In the current race to design fast, dense and energy-efficient information storage devices, spintronics (electronics that exploit the spin property of electrons) are on the lookout for ever smaller bits that move quickly within their substrate, are easily manipulated, and stable. Recently, the stabilization of ultra-small magnetic textures in synthetic antiferromagnets (SAF) have raised the scientists’ interest. The SAFs advantages are numerous: they are resistant to the external magnetic field (stable) and the longitudinal displacement speed of magnetic textures is high. But studying these promising candidates is complex using standard analysis techniques, because of the overall zero net magnetization of SAF multilayers.
The circular dichroism in X-ray resonant magnetic scattering (XRMS) technique, implemented on the SEXTANTS beamline, has allowed the measurement of several crucial parameters of these materials.
The promise of a high-density data storage medium, that is resistant to electric and magnetic fields, has raised the interest of scientists in SAF samples. The antiferromagnetic coupling of these materials is obtained through a metallic non-magnetic spacer layer, Pt|Ru, sandwiched between two ferromagnetic layers.
Scientists from Université Mixte de Physique CNRS, Thales, Univ. Paris-Saclay and a team from Pontifica Universidad Católica de Valparaíso (Chile) have tuned the layers’ composition, the stack order and the layers’ thickness in order to stabilize a spin spiral magnetic texture at room temperature (Fig1). Maximizing the “Dzyaloshinskii-Moriya interaction” (DMI) is crucial to obtain ultrasmall chiral magnetic texture. Combined with the dipolar field cancellation in SAFs, it opens the path to the stabilization of 10’s of nm diameter skyrmions (nanoscopic magnetic vortex, potential carriers of information). However, studying such structure in SAFs with standard laboratory techniques is extremely challenging due to the zero net magnetic moment in the sample.
Recently, it has been shown (https://www.synchrotron-soleil.fr/en/news/chiral-or-not-chiral-thats-question) that circular dichroism XRMS is a powerful technique to directly access the effective chirality in ferromagnetic (FM) systems using the sum and difference of images taken with circular left (CL) and circular right (CR) polarized beams at energies corresponding to specific transition edges (here Fe L edge). The work resulting from this scientific collaboration shows that the approach is also valid for SAF samples by measuring the dichroism at position in reciprocal space corresponding to the antiferromagnetic periodicity.
Moreover, the same team developed a new approach that gives rise to a quantitative information on the average magnetic texture (spin spiral) in the studied sample. Moreover, The scientists demonstrated that the period and the signal amplitude of the spin spiral is temperature independent.
In a broader perspective, circular dichroism in x-ray scattering appears to be a unique tool to study chiral magnetic texture in SAF materials. It opens the way for time resolved studies of magnetic texture in antiferromagnets or SAF samples as shown recently in FM multilayers using free electron laser facilities or high harmonic generation sources.
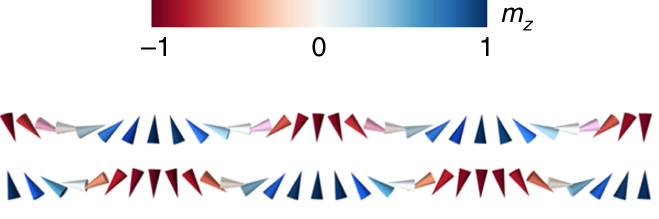
Figure 1: Result of a simulation of a SAF made of two antiferromagnetically coupled ferromagnetic layers, displaying a spin spiral, as seen from the side in the plane. In-plane and out-of-plane directions not to scale, extracted from Legrand et al. Nat. Mater. 19, 34–42 (2020).
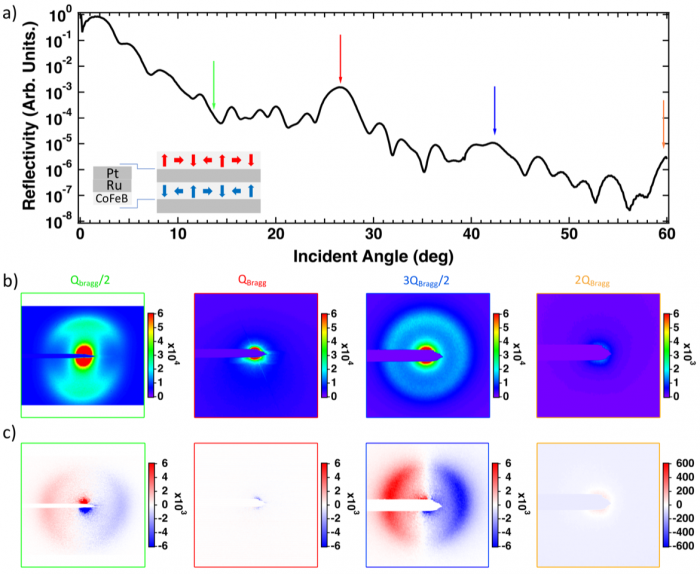
Figure 2: CD-XRMS study of a film made of 10 repetitions of a CoFeB/Ru/Pt trilayer at 300K and 707 eV photon energy (Fe L3 edge). (a) X-ray reflectivity curve using the sum (CL+CR) of the two circular polarizations. The vertical red and orange arrows point toward the position of first and second Bragg peaks. Green and blue arrows correspond to the chemical half Bragg peaks. (b) The sum images (CL+CR) corrected from the from the geometrical projection due to photon incidence angle. The magnetic scattering signal is maximum at half-integer Bragg peaks in reciprocal space and vanishes at the chemical periodicity. (c) The corresponding difference images (CL-CR) also geometrically corrected. The magnetic signal extincts at the Bragg peaks and is maximum at half-integer Bragg peaks.
