Dans un article publié récemment dans Physical Review, un groupe international de chercheurs a démontré que les distributions angulaires des électrons dans le référentiel du laboratoire pouvaient être utilisées comme outil pour sonder l'environnement chimique de l'atome depuis lequel l'électron a été émis. Les chercheurs ont mesuré les électrons émis par des molécules de chloroéthane en phase gazeuse à deux angles différents (0° et 90°) par rapport au vecteur polarisation du rayonnement synchrotron, et ont extrait de ces mesures ce que l’on nomme le paramètre d'asymétrie b des photoélectrons. Il a été observé que ce paramètre β variait de façon remarquable suivant le nombre d'atomes de chlore présents dans la molécule. En se basant sur des calculs théoriques de haut niveau, les chercheurs ont proposé un modèle physique simple pour le comportement observé du paramètre d'asymétrie, où la diffusion des photoélectrons joue un rôle essentiel.
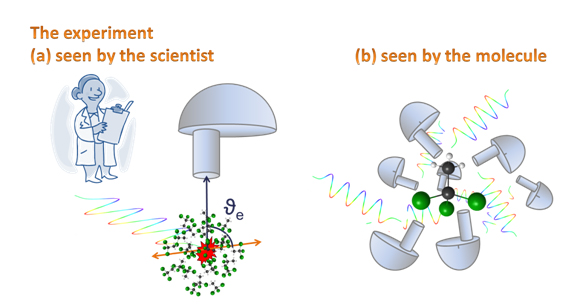
De nombreux spécialistes de la spectroscopie d’électrons sont d'avis que les distributions angulaires comptent parmi les observables (quantités mesurables) les plus difficiles à comprendre, mais aussi parmi les plus riches en informations. Que signifie la distribution angulaire en spectroscopie d’électrons ? Il s'agit de la distribution des directions suivant lesquelles les électrons sont émis dans un système de coordonnées spécifique. Est-il contre-intuitif d'affirmer que les électrons émis depuis un échantillon gazeux constitué d'objets orientés au hasard (même les molécules les plus lourdes de cette étude traversent le volume d’interaction vu par le spectromètre à plus de 800 km/h en tournant) présentent des directions d’émission préférentielles, avec davantage d'électrons détectés à certaines angles ? Si vous avez répondu oui, vous êtes sur la bonne voie et nous vous prions de continuer votre lecture. Essayons de comprendre ce qui se passe ! Il existe ici des points clés que nous devons prendre en considération : 1) comment les électrons émis ressentent le mouvement de la molécule ; 2) quel pourrait être le système de coordonnées spécifique mentionné ci-dessus ?
Tentons de répondre à ces questions en commençant par la plus facile : à l'échelle de temps de l'émission des électrons, les molécules sont presque immobiles. Les mouvements moléculaires peuvent être divisés en trois catégories, qui sont toutes associées à différentes énergies et échelles de temps : mouvements de translation, vibration, et rotation. Le mouvement de translation décrit comment le centre de masse de la molécule (la molécule dans son ensemble étant décrite comme une masse ponctuelle) bouge dans l'espace. Si l'électron est émis par une molécule volant vers le détecteur à 800 km/h, l'énergie cinétique de l'électron sera plus élevée que lorsque la molécule vole dans la direction opposée. Dans les mesures, on peut observer ce phénomène par l'élargissement des distributions d'énergie cinétique des électrons mesurés, ce qui s’appelle élargissement Doppler translationnel. Ce phénomène est globalement très semblable à l'effet Doppler « macroscopique », observé par exemple dans les ondes sonores : le bruit d'une voiture de police qui se rapproche de l’observateur est plus aigu que celui d'une voiture qui s'éloigne. Comme les molécules de l'échantillon gazeux de cette étude sont orientées au hasard, l'effet Doppler translationnel ne fait qu'élargir la distribution des énergies cinétiques (il y a le même nombre de molécules volant vers le détecteur et vers l’opposé), sans introduire d'asymétrie.[1] L'effet est faible : au pire, pour la molécule la plus légère étudiée dans l’article de Patanen et al., avec l'énergie cinétique la plus élevée pour l'électron (308 eV), l'effet Doppler translationnel ajoute un élargissement supplémentaire de 0,027 eV à la distribution des énergies des électrons.
Hormis les électrons, les noyaux de la molécule sont eux aussi des objets obéissant aux mêmes lois de la mécanique quantique. Ceci implique par exemple que les noyaux se déplacent en permanence les uns par rapport aux autres, et que l'énergie de ce mouvement est quantifiée ; le mouvement peut seulement avoir certaines énergies, nommées énergies vibrationnelles. Cette situation est comparable à un ressort pouvant être étiré de 5, 10 ou 15 cm, mais pas de 12 cm. Les états stationnaires autorisés sont nommés niveaux vibrationnels. Comment les vibrations affectent-elles les énergies des électrons ? Comme les électrons sont beaucoup plus légers que les noyaux et donc beaucoup plus rapides, ils s'adaptent immédiatement aux variations du potentiel moléculaire induites par les variations de distance entre les noyaux causées par les vibrations. Par contre, lorsqu'un électron est ionisé depuis une orbitale de cœur par un photon X, les noyaux sont si lents qu'ils ne réagissent pas immédiatement ; mais à l'instant précis de la création de l'état de cœur, la molécule a la même géométrie que la molécule neutre initiale. Pendant l'ionisation, cependant, une partie de l'énergie du photon peut passer dans l'excitation des niveaux vibrationnels de la molécule ionisée. Dans ce cas, une quantité moindre d'énergie cinétique sera disponible pour l'électron émis, conformément à la loi de conservation de l'énergie. Comme les énergies des niveaux vibrationnels sont quantifiées, il se produit des pertes d'énergie discrètes dans les électrons émis et il est alors possible d'observer une série de pics correspondant à la photoionisation d’une seule orbitale. Dans leur étude, les auteurs de l’article n'ont pas examiné les pics vibrationnels individuellement, mais tous en même temps, et l'asymétrie observée ne peut donc pas être due à l'asymétrie vibrationnelle.[2] Le troisième mouvement, celui de rotation, cause également un élargissement de la distribution d'énergie cinétique par élargissement Doppler rotationnel, de manière semblable à l'élargissement Doppler translationnel mais avec un effet généralement plus faible (ref 1).
Figure 1 - Dans la mesure des distributions angulaires des photoélectrons, l'angle entre le vecteur polarisation du rayonnement synchrotron (flèche orange à deux pointes) et l'axe de détection des électrons (flèche bleue) était de 90° ou de 0°. (a) L'observateur voit les molécules orientées au hasard, mais la position du détecteur et l'orientation du vecteur polarisation de la lumière sont fixes. (b) La molécule voit des « paires » de rayonnement synchrotron et de détecteur d'électrons avec un angle fixe entre ces deux objets, et en moyennant dans le temps, ces paires apparaissent comme étant orientées au hasard autour de la molécule. Les sphères noires sont des atomes de carbones, les sphères vertes des atomes de chlore et les petites sphères blanches des atomes d'hydrogène.
L'autre point clé consiste à sélectionner le système de coordonnées : nous observons les distributions angulaires dans un système de coordonnées qui est défini par le vecteur polarisation de la lumière synchrotron et l'axe de détection des électrons. Ceci est le référentiel du laboratoire. Le lecteur se souviendra de l'importance qu'a la définition d'un système de coordonnées adéquat dans la relativité restreinte d'Einstein, ainsi que de la façon dont cette définition influence les résultats des mesures. Imaginez un chercheur du synchrotron en weekend, prenant l'Eurostar vers Londres : sa vitesse par rapport à un pêcheur sur la côte de Calais est de 300 km/h. Cependant, dans son propre système de coordonnées, ce chercheur est immobile et c'est le pêcheur de Calais qui se déplace à grande vitesse. Dans nos mesures, le référentiel du laboratoire est défini par le vecteur polarisation du rayonnement synchrotron et l'axe de détection du spectromètre d'électrons. Dans ce système de coordonnées, notre échantillon en phase gazeuse est orienté au hasard : comme nous l'avons indiqué ci-dessus, même les molécules les plus lourdes volant à plus de 800 km/h. Y a-t-il une contradiction entre l'orientation aléatoire de l'échantillon et le premier point clé qui affirmait que les molécules étaient immobiles à l'échelle de temps de l'émission des électrons ? Non, car l'événement de photoionisation « prend des clichés » de cet ensemble de molécules orientées au hasard, et statistiquement nous effectuons la moyenne sur toutes les orientations possibles des molécules. Un autre système de coordonnées couramment utilisé en spectroscopie de photoélectrons est le référentiel moléculaire, ce qui implique que le système de coordonnées se déplace avec la molécule dans l'espace, ou plus exactement le laboratoire (détecteur d'électrons, rayonnement synchrotron) se déplace ![3]
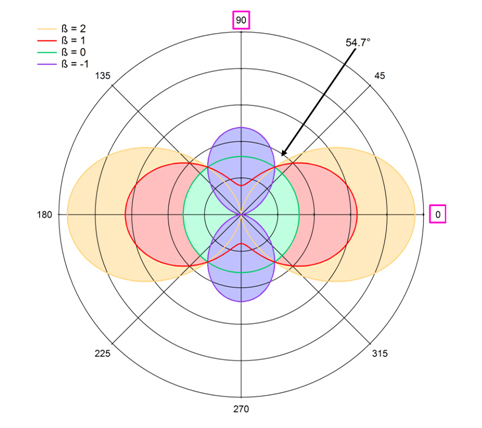
Pour comprendre l'importance du paramètre β évoqué au début, commençons par considérer un atome de carbone isolé. En principe, dans un cas idéal, la distribution angulaire des photoélectrons C 1s d'un atome de carbone devrait pouvoir être décrite par un paramètre β = 2, comme représenté sur la courbe orange de la figure 2. Sur cette courbe, l'angle polaire est l'angle entre le vecteur polarisation et l'électron émis. Nous constatons que dans ce cas, les électrons sont émis préférentiellement suivant le vecteur polarisation. Si β = 0, la distribution angulaire est complètement isotrope. À l'autre extrême, si β = -1, le maximum de la distribution est perpendiculaire au vecteur polarisation. Il est utile de signaler que cette discussion est vraie dans le cadre de l'approximation dipolaire. Cette approximation est valide si la longueur d'onde de la lumière est beaucoup plus grande que les dimensions des atomes (l'onde ne varie pas à l'intérieur de l'atome). La longueur d'onde de rayonnement la plus faible utilisée dans l'étude de Patanen et al. était de 2,1 nm, tandis que la molécule entière est environ 10 fois plus petite. Il est donc raisonnable de supposer que l'approximation dipolaire est valide.
Figure 2 - Représentation polaire de la section efficace différentielle des photoélectrons avec quatre valeurs différentes de β. L'angle polaire θ est l'angle entre le vecteur polarisation de la lumière et le vecteur vitesse de l'électron (axe du détecteur d'électrons). La flèche pointe dans la direction de l'angle 54,7°, auquel les sections efficaces sont les mêmes indépendamment de β (cet angle est si important en spectroscopie électronique qu'il est appelé angle magique). Les valeurs des angles utilisés dans la mesure de Patanen et al. sont indiquées par des rectangles roses.
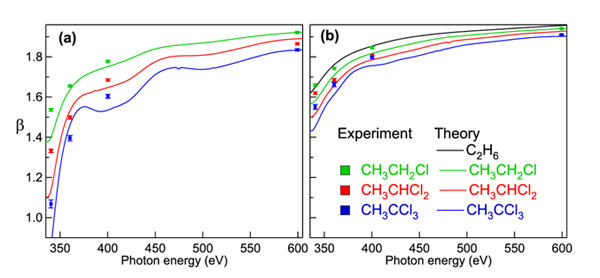
On pourrait donc s'attendre à détecter un grand nombre d'électrons en effectuant une mesure à un angle de 0°, et très peu d'électrons à 90°. En principe, c'est bien ce qui a été observé. Cependant, la différence entre les angles 0° et 90° était plus faible que la valeur attendue, et variait en fonction de l'énergie de photon. À partir des intensités mesurées, les chercheurs ont été en mesure d'extraire le paramètre β présenté dans la Figure 3 avec les calculs théoriques. La figure 3 a) présente le résultat pour l'atome de carbone substitué avec des atomes de chlore, et la figure 3 b) pour le carbone du groupe méthyle, dans une série de chloroéthanes. On constate que plus le nombre d'atomes de chlore augmente dans la molécule, plus le paramètre β devient différent de 2. En outre, la déviation par rapport à cette valeur est plus grande aux énergies d'ionisation les plus faibles.
Figure 3 - Paramètres d'asymétrie des photoélectrons dans des chloroéthanes pour une photoionisation du C 1s a) chloré et b) du groupe méthyle. La courbe théorique pour l'éthane est indiquée à titre de comparaison afin de disposer d'une référence « sans chlore ».
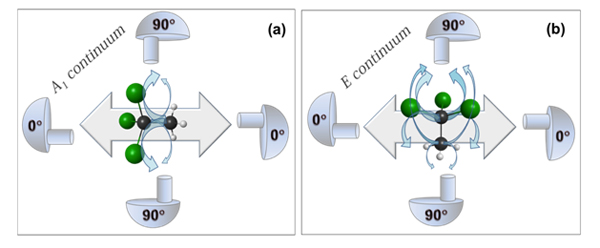
Un modèle physique décrivant l'effet de la diffusion sur les distributions angulaires des électrons est représenté dans la figure 4 pour la molécule de CH3CCl3 avec différentes polarisations et continua d'ionisation. En physique moléculaire, tout comme dans la nature en général, la symétrie d'une molécule est une propriété très importante et possède une signification physique profonde. Les molécules peuvent être classées en différents groupes de symétrie suivant leur comportement sous différentes opérations de symétrie, telles que des rotations autour d'axes et des réflexions. La symétrie de CH3CCl3 est C3v (en bref, la molécule a exactement le même aspect après une rotation de 120° autour de l'axe carbone-carbone, et d'autre part a le même aspect après une réflexion dans un plan contenant l'axe carbone-carbone et passant par l'un des atomes Cl et H). Les orbitales C 1s ont aussi leur propre symétrie et sont nommées 2a1 (C chloré) et 3a1 (C du groupe méthyle). D'après les règles de sélection dans l'approximation dipolaire, l'ionisation d'une orbitale a1 produit une onde du continuum (un photoélectron, qui obéit à la dualité onde-particule !) avec la symétrie A1 ou E. Dans l'approximation dipolaire, les photoélectrons avec la symétrie E seront préférentiellement « sélectionnés » par les molécules ayant leur axe moléculaire perpendiculaire au vecteur polarisation. Donc si le détecteur est à 90° (perpendiculaire au vecteur polarisation), aucun signal ne devrait être détecté. Dans le cas du continuum A1, les molécules ayant leur axe moléculaire parallèle au vecteur polarisation seront préférentiellement « sélectionnées » et une fois de plus, aucun signal ne devrait être détecté dans un analyseur à un angle de 90°. Toutefois, les chercheurs ont observé un signal significatif lorsque l'axe de détection des électrons et le vecteur polarisation étaient perpendiculaires entre eux. Cela leur suggère que la diffusion intramoléculaire détourne les électrons de leurs trajectoires préférentielles (flèches esquissées sur la figure 4) et que le signal à 90° augmente, ce qui rend la distribution angulaire plus isotrope et réduit ainsi la valeur du paramètre β. Plus les électrons sont lents, plus leur diffusion est probable et ainsi la valeur de β est plus éloignée de la valeur idéale 2 à faible énergie. En outre, plus la molécule contient d'atomes de chlore, plus les distributions angulaires sont isotropes. Ceci est dû aux sections efficaces de diffusion par les atomes de chlore plus élevées que celles par les atomes d'hydrogène, en raison de la taille bien inférieure de ces derniers. Il doit être signalé que l'atome de carbone voisin est aussi une source de diffusion.
En conclusion, l'étude de Patanen et al. a démontré que la diffusion électronique intramoléculaire affectait les distributions angulaires des photoélectrons dans le référentiel du laboratoire, même loin des seuils de photoionisation. La sensibilité chimique de la technique de spectroscopie de photoélectrons a permis d'étudier séparément le comportement des atomes substitués et non substitués au sein d'une molécule, exactement dans les mêmes conditions, ce qui souligne l'importance de la diffusion. Cette observation suggère qu'outre les sections efficaces totales, les distributions angulaires des électrons constituent un outil d'étude alternatif des structures moléculaires.
Figure 4 - Un modèle simple illustrant l'effet de la diffusion intramoléculaire, qui rend les distributions angulaires des photoélectrons plus isotropes dans le référentiel du laboratoire. Dans le cas du CH3CCl3, un photoélectron C 1s peut être émis sous forme d'onde a) de symétrie A1 ou b) ou de symétrie E. La double flèche indique l'orientation du vecteur polarisation, et donc la direction préférentielle d'émission des photoélectrons dans l'approximation dipolaire. Les petites flèches courbées indiquent les électrons redirigés en raison de la diffusion par les atomes voisins. Deux orientations moléculaires sont envisagées pour chaque angle entre l'axe de détection des électrons et le vecteur polarisation (0° et 90°).
[1] Toutefois, il existe des études où les molécules de l'échantillon sont (partiellement) alignées en raison d'une excitation résonnante, et présentent ainsi une asymétrie angulaire. Il s'agit cependant d'une situation différente et il est recommandé au lecteur de consulter O. Travnikova, J. C. Liu, A. Lindblad, C. Nicolas, J. Söderström, V. Kimberg, F. Gel’mukhanov & C. Miron, Circularly Polarized X Rays: Another Probe of Ultrafast Molecular Decay Dynamics, Phys. Rev. Lett. 105, 233001 (2010) ainsi que les références de cet article pour plus d'informations.
[2] On ne doit surtout pas supposer que chaque sous-niveau vibrationnel individuel présente la même asymétrie angulaire, surtout lorsque l'énergie cinétique de l'électron émis est faible (proche du seuil de photoionisation) ou que les états ionisés sont atteints via des excitations résonantes (voir par exemple A. Lindblad, V. Kimberg, J. Söderström, C. Nicolas, O. Travnikova, N. Kosugi, F. Gel’mukhanov, and C Miron, Vibrational Scattering Anisotropy in O2 – dynamics beyond the Born-Oppenheimer approximation, New J. Phys. 14, 113018 (2012).
[3] En pratique, la molécule peut être « fixée dans l'espace », par exemple en déterminant l'orientation de son axe moléculaire par rapport à la polarisation de la lumière lors de la détection des ions fragments suite à une ionisation de cœur.
Référence :
1 T. D. Thomas et al, Phys. Rev. Lett. 106, 193009 (2011).